4-1-1 Information
"2 bits, 4 bits, 6 bits a byte!"
 |
|
What is "Information"?
information, n. Knowledge communicated or received concerning a particular fact or circumstance.

A Computer Scientist's definiton:
Information resolves uncertainty.
Information is simply that which cannot be predicted. The less predictable a message is, the more information it conveys!

Quantifying Information
(Claude Shannon, 1948)
Suppose you're faced with N equally probable choices, and I give you a fact that narrows it down to M choices. Then you've been given:

log2(N/M) bits of information
Examples:
- Outcome of one coin flip: log2(2/1) = 1 bit
- The roll of one die: log2(6/1) = ~2.6 bits
- Someone tells you that their 7-digit phone number is a palindrome?
log2(107/104) = ~9.966 bits
Another Eample: Sum of 2 dice
 |
i2 = log2(36/1) = 5.170 bits
i3 = log2(36/2) = 4.170 bits i4 = log2(36/3) = 3.585 bits i5 = log2(36/4) = 3.170 bits i6 = log2(36/5) = 2.848 bits i7 = log2(36/6) = 2.585 bits i8 = log2(36/5) = 2.848 bits i9 = log2(36/4) = 3.170 bits i10 = log2(36/3) = 3.585 bits i11 = log2(36/2) = 4.170 bits i12 = log2(36/1) = 5.170 bits |
The average information provided by the sum of 2 dice is: 3.274 bits.
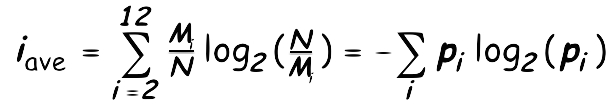
The average information from events of given process is called its Entropy.
Show me the bits!
- Is there a concrete ENCODING that achieves the information content?
- Can the sum of two dice REALLY be represented using 3.274 bits?
- If so, how?
- The fact is, the average information content is a strict lower-bound on how small of a representation that we can achieve.
- In practice, it is difficult to reach this bound. But, we can come very close.

Variable-Length Encoding
- Of course we can use differing numbers of "bits" to represent each item of data
- This is particularly useful if all items are not equally likely
- Equally likely items lead to fixed length encodings:
- Ex. Encode a "particular" roll of 5?
- {(1,4),(2,3),(3,2),(4,1)} which are equally likely if we use fair dice
- 00 = (1,4), 01 = (2,3), 10 = (3,2), 11 = (4,1)
- Back to the original problem. Let's use this encoding:
| 2 = 10011 | 3 = 0101 | 4 = 011 | 5 = 001 |
| 6 = 111 | 7 = 101 | 8 = 110 | 9 = 000 |
| 10 = 1000 | 11 = 0100 | 12 = 10010 |
Variable-Length Decoding
| 2 = 10011 | 3 = 0101 | 4 = 011 | 5 = 001 |
| 6 = 111 | 7 = 101 | 8 = 110 | 9 = 000 |
| 10 = 1000 | 11 = 0100 | 12 = 10010 |

- Notice how unlikely rolls are encoded using more bits, whereas likely rolls use fewer bits
- Let's use our encoding to decode the following bit sequence:
- Where did this code come from?
(Click in box to decode)
1001100101011110011100101
2
1001100101011110011100101
2 5
1001100101011110011100101
2 5 3
1001100101011110011100101
2 5 3 6
1001100101011110011100101
2 5 3 6 5
1001100101011110011100101
2 5 3 6 5 8
1001100101011110011100101
2 5 3 6 5 8 3
1001100101011110011100101
Huffman Coding
A simple greedy algorithm for approximating a minimum encoding
- Find the 2 items with the smallest probabilities
- Join them into a new *meta* item whose probability is their sum
- Remove the two items and insert the new meta item
- Repeat from step 1 until there is only one item

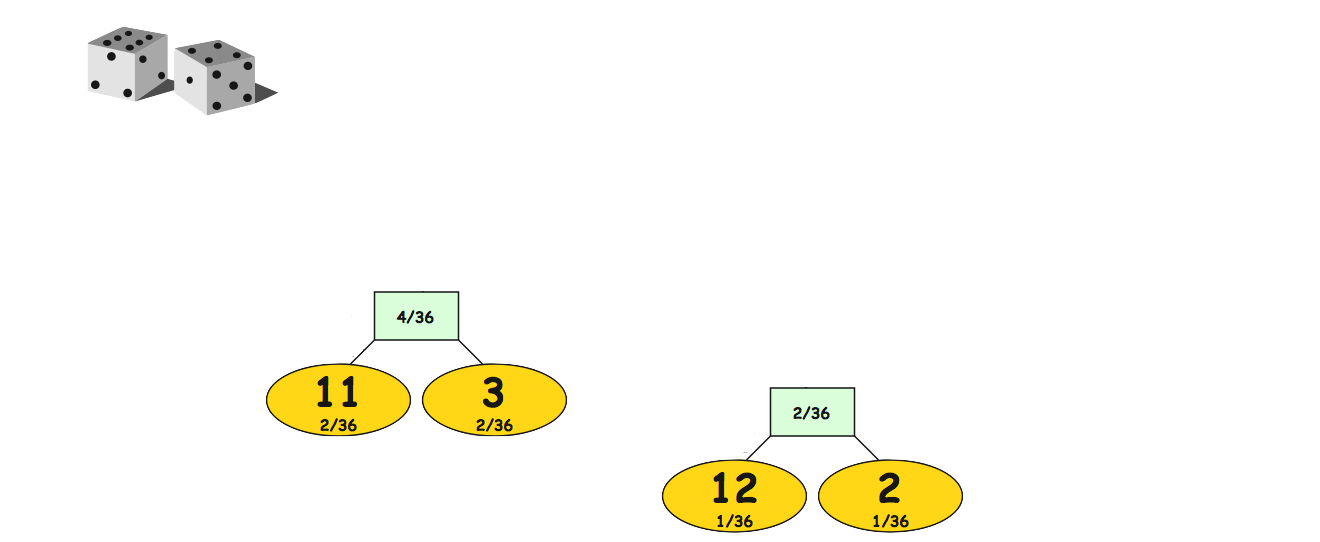

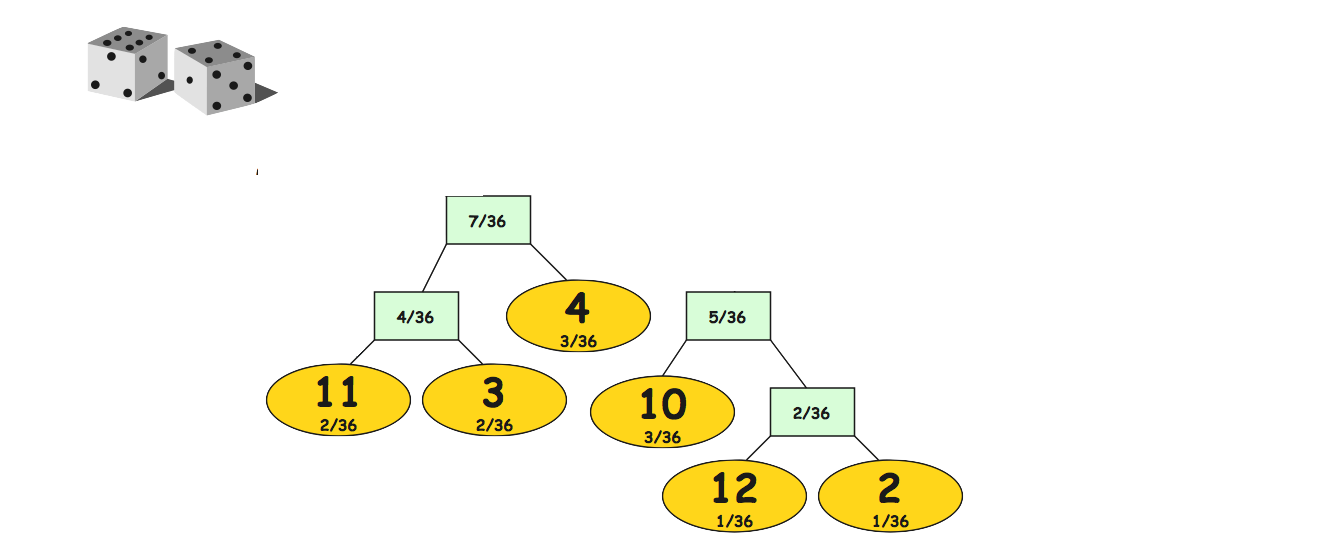

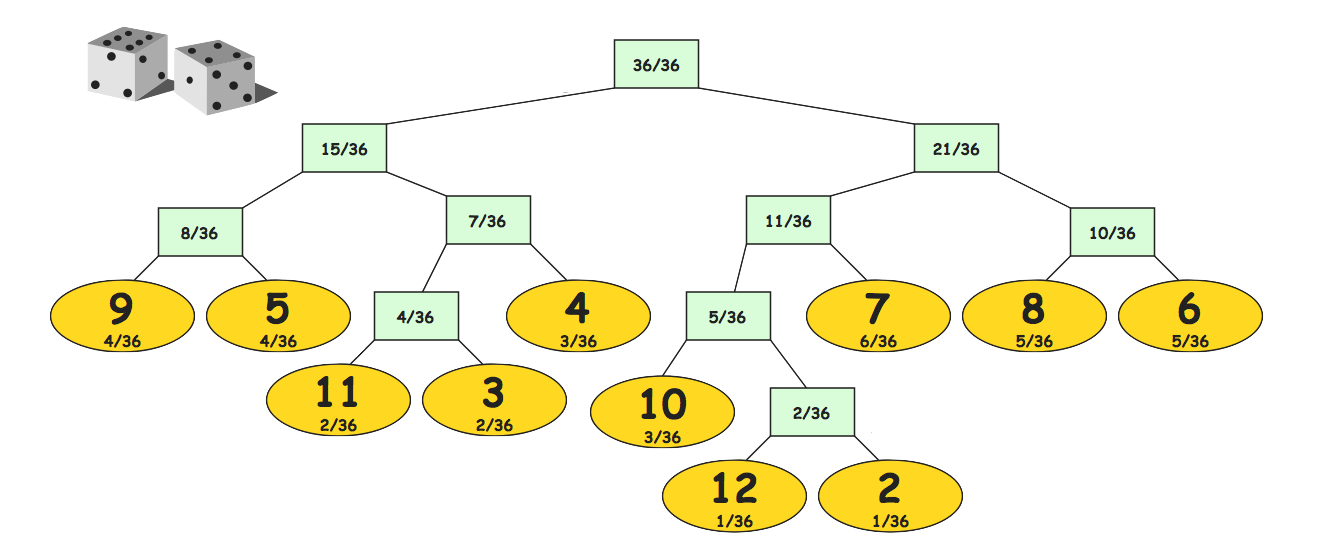
Converting Tree to an Encoding
Once the *tree* is constructed, label its edges consistently and follow the paths from the largest *meta* item to each of the real item to find the encoding.
| 2 = 10011 | 3 = 0101 | 4 = 011 | 5 = 001 |
| 6 = 111 | 7 = 101 | 8 = 110 | 9 = 000 |
| 10 = 1000 | 11 = 0100 | 12 = 10010 |

Coding Efficiency
How does this code compare to the information content?
Pretty close. Recall that the lower bound was 3.274 bits.
However, an efficient encoding (as defined by having an average code size close to the information content) is not always what we want!
Encoding Considerations
- Encoding schemes that attempt to match the information content of a data stream remove redundancy. They are data compression techniques.
- However, sometimes our goal in encoding information is increase redundancy, rather than remove it. Why?
- Make the information easier to manipulate (fixed-sized encodings)
- Make the data stream resilient to noise (error detecting and correcting codes)


Information Encoding Standards
- "Encoding" is the process of assigning representations to information
- Choosing an appropriate and efficient encoding is an engineering challenge
(and an art) - Impacts design at many levels
- Mechanism (devices, # of components used)
- Efficiency (# bits used)
- Reliability (tolerate noise)
- Security (encryption)

Fixed-Size Codes
If all choices are equally likely (or we have no reason to expect otherwise), then a fixed-size code is often used. Such a code should use at least enough bits to represent the information content.
| BCD | |
| 0 - | 0000 |
| 1 - | 0001 |
| 2 - | 0010 |
| 3 - | 0011 |
| 4 - | 0100 |
| 5 - | 0101 |
| 6 - | 0110 |
| 7 - | 0111 |
| 8 - | 1000 |
| 9 - | 1001 |
ex. Decimal digits 10 = {0,1,2,3,4,5,6,7,8,9}
4-bit BCD (binary code decimal)
log2(10/1) = 3.322 < 4 bits
ex. ~84 English characters = {A-Z (26), a-z (26), 0-9 (10),
punctuation (8), math (9), financial (5)}
7-bit ASCII (American Standard Code for Information Interchange)
log2(84/1) = 6.392 < 7 bits
ASCII
| 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 000 | NUL | SOH | STX | ETX | EOT | ACK | ENQ | BEL | BS | HT | LF | VT | FF | CR | SO | SI |
| 001 | DLE | DC1 | DC2 | DC3 | DC4 | NAK | SYN | ETB | CAN | EM | SUB | ESC | FS | GS | RS | US |
| 010 | ! | " | # | $ | % | & | ' | ( | ) | * | + | , | - | . | / | |
| 011 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | : | ; | < | = | > | ? |
| 100 | @ | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O |
| 101 | P | Q | R | S | T | U | V | W | X | Y | Z | [ | \ | ] | ^ | _ |
| 110 | ` | a | b | c | d | e | f | g | h | i | j | k | l | m | n | o |
| 111 | p | q | r | s | t | u | v | w | x | y | z | { | | | } | ~ | DEL |
- For letters upper and lower case differ in the 6th "shift" bit
10XXXXX is upper, and 11XXXXX is lower - Special "control" characters set upper two bits to 00
ex. cntl-g → bell, cntl-m → carriage return, cntl-[ → esc - This is why bytes have 8-bits (ASCII + optional parity). Historically, there were computers built with 6-bit bytes, which required a special "shift" character to set case.
Unicode
- ASCII is biased towards western languages. English in particular.
- There are, in fact, many more than 256 characters in common use:
â, ö, ß, ñ, è, ¥, £, 揗, 敇, 횝, カ, ℵ, ℷ, ж, క - Unicode is a worldwide standard that supports all languages, special characters, classic, and arcane.
- Several encoding variants 16-bit (UTF-8)
- Variable length (as determined by first byte)

Encoding Positive Integers
It is straightforward to encode positive integers as a sequence of bits. Each bit is assigned a weight. Ordered from right to left, these weights are increasing powers of 2. The value of an n-bit number encoded in this fashion is given by the following formula:
| 211 | 210 | 29 | 28 | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |

Favorite Bits
- You are going to have to get accustomed to working in binary. Specifically for Comp 411, but it will be helpful throughout your career as a computer scientist.
- Here are some helpful guides:
1. Memorize the first 10 powers of 2
2. Memorize the prefixes for powers of 2 that are multiples of 1020 = 1 25 = 32 21 = 2 26 = 64 22 = 4 27 = 128 23 = 8 28 = 256 24 = 16 29 = 512
210 = Kilo (1024) 220 = Mega (1024*1024) 230 = Giga (1024*1024*1024) 240 = Tera (1024*1024*1024*1024) 250 = Peta (1024*1024*1024*1024*1024) 260 = Exa (1024*1024*1024*1024*1024*1024)
Tricks wit Bits
- The first thing that you'll do a lot of is cluster groups of contiguous bits.
- Using the binary powers that are multiples of 10 we can do the most basic clustering.
- When you convert a binary number to decimal, first break it down frome the right into clusters of 10 bits.
- Then compute the value of the leftmost remaining bits (1)
- Find the appropriate prefix (GIGA)
- Often this is sufficient (might need to round up)

A "Giga" something or other
Other Helpful Clusterings
Oftentimes we will find it convenient to cluster groups of bits together for a more compact written representation. Clustering by 3 bits is called Octal, and it is often indicated with a leading zero, 0. Octal is not that common today.

One Last Clusterings
Clusters of 4 bits are used most frequently. This representation is called hexadecimal. The hexadecimal digits include 0-9, and A-F, and each digit position represents a power of 16. Commonly indicated with a leading "0x".

Summary and Next Time
- Information is all about bits, Entropy
- Using bits to encode things
- Effficent variable-length encodings
- Redundancy
- Next: more about encoding numbers
- Signed Numbers (there is a choice)
- Non-integers (Fractions and Fixed-point)
- Floating points
- Encoding other things...